L’algorithme de débruitage mis en place repose sur une régularisation adaptative de l’algorithme des NL-means [1]. Le modèle proposé est le suivant :
(1) 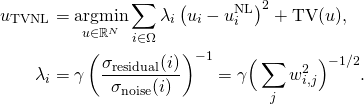
où ![]() est la solution obtenue par l’algorithme de NL-means, TV désigne la variation totale de l’image et
est la solution obtenue par l’algorithme de NL-means, TV désigne la variation totale de l’image et ![]() est le poids qui mesure la similarité entre le patch d’indice
est le poids qui mesure la similarité entre le patch d’indice ![]() et le patch d’indice
et le patch d’indice ![]() dans l’algorithme des NL-means. Le rapport
dans l’algorithme des NL-means. Le rapport ![]() traduit la réduction de la variance du bruit assurée par les NL-means. Cette formulation permet de régulariser localement et de façon adaptative la solution
traduit la réduction de la variance du bruit assurée par les NL-means. Cette formulation permet de régulariser localement et de façon adaptative la solution ![]() obtenue par les NL-means, en se basant sur un indice de confiance
obtenue par les NL-means, en se basant sur un indice de confiance ![]() qui traduit la qualité du débruitage effectué par les NL-means.
qui traduit la qualité du débruitage effectué par les NL-means.
Ce modèle s’adapte aux différentes statistiques de bruit de la famille exponentielle (Gaussien, Poisson, multiplicatif…). Il est également adapté au débruitage vidéo grâce à l’utilisation de patchs 3D combinée à une régularisation TV spatio-temporelle.
Résultats et comparaisons de débruitage de vidéos avec R-NL
Publications asosciées :
– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Adaptive regularization of the NL-means : Application to image and video denoising. IEEE Transactions on image processing, vol. 23(8) : 3506-3521, 2014.
– C. Sutour, J.-F. Aujol, C.-A. Deledalle et J.-P. Domenger. Adaptive regularization of the NL-means for video denoising. International Conference on Image Processing (ICIP), pages 2704–2708. IEEE, 2014.
– C. Sutour, J.-F. Aujol et C.-A. Deledalle. TV-NL : Une coopération entre les NL-means et les méthodes variationnelles. Gretsi, 2013.
Références
[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.