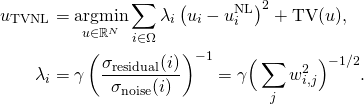Archives de catégorie : [:fr]traitement d’images[:en]image processing

Axe 4 : Approches parcimonieuses, non-locales, par patchs et analyse harmonique

Cet axe de recherche est motivé par la problématique de l’analyse de données en grande dimension (signaux et images) organisées sous la forme de vecteurs ou matrices de grande taille.

Une première partie de cet axe porte sur les approches parcimonieuses permettant l’analyse de données en grande dimension lorsque celles-ci peuvent être bien approchées dans un espace de faible dimension. On s’intéresse alors à l’élaboration de modèles variationnels qui promeuvent naturellement cette parcimonie pour une représentation choisie au préalable (ondelettes, champs de gradients, etc.) ou appris sur un jeu de donnée externe. Cette représentation (l’espace de faible dimension) peut être aussi sélectionnée par le modèle lui-même, on parle alors d’apprentissage de dictionnaires qui généralement s’exprime comme un problème de factorisation de matrices. A titre d’exemples, nous nous intéressons aux méthodes d’approximation par seuillage d’ondelettes en traitement d’images, ainsi qu’aux problèmes de sélection de variables par Lasso (pour Least Absolute Shrinkage and Selection Operator). Au delà de l’élaboration de tels modèles, on cherche à comprendre leur comportement. En particulier, dans le premier exemple, on s’intéresse aux conditions assurant qu’une signal puisse être reconstruit, ou bien que son erreur de reconstruction puisse être bornée (robustesse). Dans le second exemple, on se focalise sur les conditions assurant l’identification des bonnes variables.

Une seconde partie concerne, l’analyse des motifs récurrents dans le cas des images ou de signaux multidimensionnels. Ces récurrences fournissent en effet une information clé pour le traitement ou l’interprétation de l’information. En particulier, on s’intéresse aux approches non-locales en imagerie qui s’appuient sur la similarité des motifs via des patchs (petites fenêtres généralement rectangulaires de taille 8 par 8 pixels). Le terme non-local signifie ici que seul le contenu du patch est pertinent, peu importe sa localisation spatiale. Une part de notre travail porte sur la construction et le choix des métriques pour la mise en correspondance robuste des motifs ainsi que sur la mise en place d’algorithmes de recherche efficaces. On s’intéresse par la suite à l’analyse de ces récurrences, typiquement sur le graphes des connections. Finalement, on cherche à élaborer puis étudier de nouveaux modèles variationnels prenant compte de ces informations non-locales.

Axe 3 : Le guidage des thérapies par l’imagerie

Ces activités s’inscrivent dans le cadre de la radiologie interventionnelle, discipline en plein essor, pour laquelle la France se range au premier plan dans le monde. La possibilité de déposer localement une énergie de manière non-invasive ouvre une nouvelle voie vers des stratégies thérapeutiques pour les tumeurs malignes plus fiables, moins agressives pour les patients, qui permettront une réduction des temps et des coûts d’hospitalisation. Dans ce cadre, une activité de l’équipe IOP s’est orientée autour des méthodes de traitements d’images en temps réel, permettant le guidage par imagerie (IRM ou échographique) d’un traitement de manière mini ou non-invasive (ablation thermique ou radiothérapie), permettant aussi le dépôt local de médicaments.

Axe 2 : Transport optimal pour le traitement du signal et des images

Cet axe est centré sur le développement de nouvelles méthodologies pour l’analyse de données de grande taille tels que des histogrammes, images ou nuages de points, à partir de concepts issus de la théorie du transport optimal. Cette méthodologie conduit à l’utilisation de métriques non-euclidiennes (du type distances de Wasserstein) afin d’extraire de l’information géométrique en présence de sources de variabilité non-linéaires dans des données. Dans ce cadre, une nouvelle méthode d’Analyse en Composantes Principales basée sur la distance de Wasserstein a été récemment proposée avec des applications pour l’analyse statistique d’histogrammes.

L’utilisation du transport optimal a également été proposée pour différents problèmes de traitement d’images. En généralisant les distances de transport par régularisation des plans de transport associés, de nouvelles méthodes d’interpolations d’images ont été développées pour des applications en océanographie. La distance de Wasserstein a également été considérée pour des problèmes plus classiques d’image tels que la segmentation ou le transfer de couleur.

Axe 1 : Méthodes variationnelles et régularisation

Les méthodes variationnelles sont très utilisées en traitement d’image. Elles permettent en effet de proposer des modèles tenant compte des spécificités des problèmes considérés. Elles permettent aussi l’étude des propriétés des solutions. Les fonctionnelles proposées en traitement d’image sont non lisses (pour tenir compte de la présence d’interfaces), et pas nécessairement convexes. Il se pose naturellement des questions d’existence de solutions, d’unicité éventuelle, de calcul (rapide) des solutions. Le choix de la régularisation est souvent basé sur une hypothèse de parcimonie (e.g., du gradient, ou dans un domaine transformé). Les interactions non locales et la notion de patch interviennent classiquement dans la construction des fonctionnelles. Enfin, toutes ces approches reposent en principe sur la pondération entre le terme d’attaches aux données et le terme de régularisation, ce qui conduit à la question de l’estimation fiable de ce paramètre.

Estimation de coûts au sens de Kullback-Leibler

Nous abordons la question de l’estimation des coûts au sens de Kullback-Leibler comme une alternative aux coûts quadratiques dans les problèmes de reconstruction où le bruit est distribué au sein de la famille exponentielle. Nous identifions les conditions dans lesquelles ces coûts peuvent être estimés sans biais avec avec un biais contrôlée. Des simulations sur des problèmes de sélection de paramètres dans des applications de débruitage d’images avec du bruit Gamma et Poisson illustrent l’intérêt des coûts au sens de Kullback-Leibler et des estimateurs proposés.

Article disponible ici

Convergence de FISTA

Charles Dossal a démontré avec Antonin Chambolle en 2015 la convergence d’un algorithme extrêmement populaire depuis son introduction en 2008 par Beck et Teboulle (car étant extrêmement performant en pratique), l’algorithme FISTA (Fast Iterative Shrinkage Algorithm). La convergence de cet algorithme est restée un problème ouvert dans les communautés optimisation/compressed sensing/traitement d’images/machine learning pendant 7 ans, jusqu’au travail de Charles Dossal.

Scale-Space and Variational Methods

L’équipe a organisé début juin 2015 la conférence internationale SSVM 2015 (Scale-Space and Variational Methods in Image Processing) sur le bassin d’Arcachon. Plus de 120 chercheurs venus du monde entier ont participé. Les actes de la conférence ont été publiés dans un livre par Springer.

Estimation non paramétrique du bruit

Afin de fournir un algorithme de débruitage automatique, nous avons développé une méthode automatique d’estimation du bruit dans une image, basée sur la détection non paramétrique des zones homogènes. Les régions homogènes de l’image sont détectées à l’aide du coefficient de corrélation de rang de Kendall [1]. Evalué sur des séquences de pixels voisins, il permet de mesurer la dépendance entre voisins et donc la présence de structure au sein d’un bloc de l’image.
Ce test est non paramétrique, donc la performance du détecteur est indépendante de la distribution statistique du bruit. Une fois les zones homogènes détectées, la fonction de niveau de bruit, c’est-à-dire la fonction reliant la variance du bruit à l’intensité sous-jacente de l’image, est estimée sous forme d’un polynôme du second degré à l’aide de la minimisation de l’erreur \ell^1 des statistiques issues de ces régions homogènes.

Codes Matlab pour l’estimation de bruit

Publications associées :

– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation of the noise level function based on a non-parametric detection of homogeneous image regions. Submitted to Siam Journal on Imaging Sciences, 2015.

– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation du niveau de bruit par la détection non paramétrique de zones homogènes. Submitted to Gretsi, 2015.

Références

[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.

Régularisation adaptative des NL-means

L’algorithme de débruitage mis en place repose sur une régularisation adaptative de l’algorithme des NL-means [1]. Le modèle proposé est le suivant :

(1)   \begin{align*} u_{\text{TVNL}} &= \underset{u \in \mathbb{R}^N}{\operatorname{argmin}} \sum_{i \in \Omega} \lambda_i \left(u_i-u^{\text{NL}}_i\right)^2 + \text{TV}(u),\\ \lambda_i &= \gamma \left(\frac{\sigma_{\text{residual}}(i)}{\sigma_{\text{noise}}(i)}\right)^{-1} = \gamma \Big(\sum_j w_{i,j}^2\Big)^{-1/2}. \end{align*}

où u_{\NL} est la solution obtenue par l’algorithme de NL-means, TV désigne la variation totale de l’image et w_{i,j} est le poids qui mesure la similarité entre le patch d’indice i et le patch d’indice j dans l’algorithme des NL-means. Le rapport \left(\frac{\sigma_{\text{residual}}(i)}{\sigma_{\text{noise}}(i)}\right)^{-1} traduit la réduction de la variance du bruit assurée par les NL-means. Cette formulation permet de régulariser localement et de façon adaptative la solution u_{\NL} obtenue par les NL-means, en se basant sur un indice de confiance \lambda_i qui traduit la qualité du débruitage effectué par les NL-means.

Ce modèle s’adapte aux différentes statistiques de bruit de la famille exponentielle (Gaussien, Poisson, multiplicatif…). Il est également adapté au débruitage vidéo grâce à l’utilisation de patchs 3D combinée à une régularisation TV spatio-temporelle.

Codes Matlab pour RNL

Résultats et comparaisons de débruitage de vidéos avec R-NL

Publications asosciées :
– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Adaptive regularization of the NL-means : Application to image and video denoising. IEEE Transactions on image processing, vol. 23(8) : 3506-3521, 2014.

– C. Sutour, J.-F. Aujol, C.-A. Deledalle et J.-P. Domenger. Adaptive regularization of the NL-means for video denoising. International Conference on Image Processing (ICIP), pages 2704–2708. IEEE, 2014.

– C. Sutour, J.-F. Aujol et C.-A. Deledalle. TV-NL : Une coopération entre les NL-means et les méthodes variationnelles. Gretsi, 2013.

Références

[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.