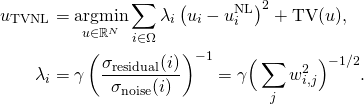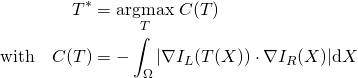Archives de l’auteur : Camille Sutour

Estimation non paramétrique du bruit

Afin de fournir un algorithme de débruitage automatique, nous avons développé une méthode automatique d’estimation du bruit dans une image, basée sur la détection non paramétrique des zones homogènes. Les régions homogènes de l’image sont détectées à l’aide du coefficient de corrélation de rang de Kendall [1]. Evalué sur des séquences de pixels voisins, il permet de mesurer la dépendance entre voisins et donc la présence de structure au sein d’un bloc de l’image.
Ce test est non paramétrique, donc la performance du détecteur est indépendante de la distribution statistique du bruit. Une fois les zones homogènes détectées, la fonction de niveau de bruit, c’est-à-dire la fonction reliant la variance du bruit à l’intensité sous-jacente de l’image, est estimée sous forme d’un polynôme du second degré à l’aide de la minimisation de l’erreur \ell^1 des statistiques issues de ces régions homogènes.

Codes Matlab pour l’estimation de bruit

Publications associées :

– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation of the noise level function based on a non-parametric detection of homogeneous image regions. Submitted to Siam Journal on Imaging Sciences, 2015.

– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation du niveau de bruit par la détection non paramétrique de zones homogènes. Submitted to Gretsi, 2015.

Références

[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.

Régularisation adaptative des NL-means

L’algorithme de débruitage mis en place repose sur une régularisation adaptative de l’algorithme des NL-means [1]. Le modèle proposé est le suivant :

(1)   \begin{align*} u_{\text{TVNL}} &= \underset{u \in \mathbb{R}^N}{\operatorname{argmin}} \sum_{i \in \Omega} \lambda_i \left(u_i-u^{\text{NL}}_i\right)^2 + \text{TV}(u),\\ \lambda_i &= \gamma \left(\frac{\sigma_{\text{residual}}(i)}{\sigma_{\text{noise}}(i)}\right)^{-1} = \gamma \Big(\sum_j w_{i,j}^2\Big)^{-1/2}. \end{align*}

où u_{\NL} est la solution obtenue par l’algorithme de NL-means, TV désigne la variation totale de l’image et w_{i,j} est le poids qui mesure la similarité entre le patch d’indice i et le patch d’indice j dans l’algorithme des NL-means. Le rapport \left(\frac{\sigma_{\text{residual}}(i)}{\sigma_{\text{noise}}(i)}\right)^{-1} traduit la réduction de la variance du bruit assurée par les NL-means. Cette formulation permet de régulariser localement et de façon adaptative la solution u_{\NL} obtenue par les NL-means, en se basant sur un indice de confiance \lambda_i qui traduit la qualité du débruitage effectué par les NL-means.

Ce modèle s’adapte aux différentes statistiques de bruit de la famille exponentielle (Gaussien, Poisson, multiplicatif…). Il est également adapté au débruitage vidéo grâce à l’utilisation de patchs 3D combinée à une régularisation TV spatio-temporelle.

Codes Matlab pour RNL

Résultats et comparaisons de débruitage de vidéos avec R-NL

Publications asosciées :
– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Adaptive regularization of the NL-means : Application to image and video denoising. IEEE Transactions on image processing, vol. 23(8) : 3506-3521, 2014.

– C. Sutour, J.-F. Aujol, C.-A. Deledalle et J.-P. Domenger. Adaptive regularization of the NL-means for video denoising. International Conference on Image Processing (ICIP), pages 2704–2708. IEEE, 2014.

– C. Sutour, J.-F. Aujol et C.-A. Deledalle. TV-NL : Une coopération entre les NL-means et les méthodes variationnelles. Gretsi, 2013.

Références

[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.

Recalage multi-modal basé contours

Afin d’effectuer la fusion multi-modale entre les images obtenues à partir d’un intensificateur de lumière (LI) et IR (images infra-rouge), fournissant ainsi des informations multi-sources pour le pilote, il est nécessaire d’effectuer le recalage entre les deux modalités. Elles reflètent des propriétés différentes de la scène, de sorte que la méthode choisie est basée sur l’information géométrique et les bords de chaque image.

Le but est de trouver la transformation T ^ * qui transfère l’image IL dans le cadre de référence de l’image IR en minimisant l’énergie suivante:

(1)   \begin{align*} T^* &= \underset{T}{\operatorname{argmax}} \; C(T)\\ \text{with} \quad C(T) &= - \int_{\Omega} \vert \nabla I_L(T(X)) \cdot \nabla I_R(X)\vert \mathrm dX \end{align*}

Cette mesure est basée sur les contours de chaque image, et elle prend en compte les contours des deux modalitites, ce qui la rend insensible aux valeurs aberrantes.
Grâce à un schéma d’optimisation à base de descente de gradient, il est possible d’évaluer rapidement la transformation optimale entre les deux modalités.

Résultats de recalage sur des données réelles

Related papers:
C. Sutour, J.-F. Aujol, C.-A. Deledalle et B.D. De-Senneville. Edge-based multi-modal registration and application for night vision devices. Journal of Mathematical Imaging and Vision, pages 1–20, 2015.