Vision nocturne numérique :
Restauration automatique et recalage multimodal des images à bas niveau de lumière.
Ces travaux sont réalisés dans le cadre de la thèse de Camille Sutour intitulée « Vision nocturne numérique : restauration automatique et recalage multimodal des images à bas niveau de lumière ». Cette thèse est financée par la DGA et la région Aquitaine et s’effectue en collaboration avec Thales Avionics au Haillan. L’objectif de ce projet est d’améliorer la qualité de la vision de nuit des pilotes à l’aide d’un système numérique doté d’un intensificateur de lumière (IL) couplé à une caméra CCD monté sur la visière de casque, et dont les images sont projetées directement sur la visière du casque. Les études menées consistent dans un premier temps à améliorer la qualité des images IL en effectuant une étape de débruitage, puis à recaler ces images avec des images infra-rouge (IR) pour pouvoir procéder à de la fusion de capteurs. Ces travaux s’inscrivent dans un contexte opérationnel où l’on traite un flux vidéo avec une forte contrainte temps-réel.

Etapes de traitement des images BNL. (a) Image IL brute, (b) Image IL débruitée à recaler ; les contours non alignés de l’image IR sont superposés, (c) Image IL recalée sur l’image IR, (d) Image IR.
R-NL : NL-means régularisés
Codes Matlab pour le débruitage R-NL
Résultats de débruitage vidéos R-NL
L’algorithme de débruitage mis en place repose sur une régularisation adaptative de l’algorithme des NL-means [1]. Le modèle proposé est le suivant [2] :
(1) 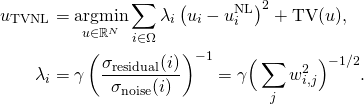
où ![]() est la solution obtenue par l’algorithme de NL-means, TV désigne la variation totale de l’image et
est la solution obtenue par l’algorithme de NL-means, TV désigne la variation totale de l’image et ![]() est le poids qui mesure la similarité entre le patch d’indice
est le poids qui mesure la similarité entre le patch d’indice ![]() et le patch d’indice
et le patch d’indice ![]() dans l’algorithme des NL-means. Le rapport
dans l’algorithme des NL-means. Le rapport ![]() traduit la réduction de la variance du bruit assurée par les NL-means. Cette formulation permet de régulariser localement et de façon adaptative la solution
traduit la réduction de la variance du bruit assurée par les NL-means. Cette formulation permet de régulariser localement et de façon adaptative la solution ![]() obtenue par les NL-means, en se basant sur un indice de confiance
obtenue par les NL-means, en se basant sur un indice de confiance ![]() qui traduit la qualité du débruitage effectué par les NL-means.
qui traduit la qualité du débruitage effectué par les NL-means.
Ce modèle s’adapte aux différentes statistiques de bruit de la famille exponentielle (Gaussien, Poisson, multiplicatif…). Il est également adapté au débruitage vidéo grâce à l’utilisation de patchs 3D combinée à une régularisation TV spatio-temporelle.
Publications associées :
1. C. Sutour, C.-A. Deledalle et J.-F. Aujol. Adaptive regularization of the NL-means : Application to image and video denoising. IEEE Transactions on image processing, vol. 23(8) : 3506-3521, 2014.
2. C. Sutour, J.-F. Aujol, C.-A. Deledalle et J.-P. Domenger. Adaptive regularization of the NL-means for video denoising. International Conference on Image Processing (ICIP), pages 2704–2708. IEEE, 2014.
3. C. Sutour, J.-F. Aujol et C.-A. Deledalle. TV-NL : Une coopération entre les NL-means et les méthodes variationnelles. Gretsi, 2013.
Plus d’information et de résultats à propos de R-NL
Recalage multi-modal
Afin de pouvoir procéder à de la fusion multi-capteurs des images IL et IR (infra-rouge) et ainsi apporter différentes sources d’information au pilote, il est nécessaire d’effectuer un recalage entre les deux modalités. Celles-ci présentent des caractéristiques très différentes, donc l’approche retenue est basée sur l’information géométrique et les contours de chaque image.
Le but est de chercher le transformation ![]() qui transforme l’image IL dans le référentiel de l’image IR en minimisant l’énergie suivante :
qui transforme l’image IL dans le référentiel de l’image IR en minimisant l’énergie suivante :
(2) 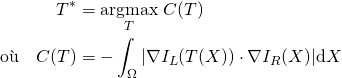
Ce critère est basé sur les contours de chacune des images, et permet de ne prendre en compte que les contours présents dans les deux modalités, ce qui le rend moins sensibles aux outliers.
À l’aide d’une optimisation basée sur une descente de gradient, il est possible de déterminer rapidement le recalage optimal entre les deux capteurs.
Publications associées :
C. Sutour, J.-F. Aujol, C.-A. Deledalle et B.D. De-Senneville. Edge-based multi-modal registration and application for night vision devices. Journal of Mathematical Imaging and Vision, pages 1–20, 2015.
Estimation non paramétrique du bruit
Codes Matlab pour l’estimation de bruit
Afin de fournir un algorithme de débruitage automatique, nous avons développé une méthode automatique d’estimation du bruit dans une image, basée sur la détection non paramétrique des zones homogènes.
Les régions homogènes de l’image sont détectées à l’aide du coefficient de corrélation de rang de Kendall [3]. Evalué sur des séquences de pixels voisins, il permet de mesurer la dépendance entre voisins et donc la présence de structure au sein d’un bloc de l’image.
Ce test est non paramétrique, donc la performance du détecteur est indépendante de la distribution statistique du bruit.
Une fois les zones homogènes détectées, la fonction de niveau de bruit, c’est-à-dire la fonction reliant la variance du bruit à l’intensité sous-jacente de l’image, est estimée sous forme d’un polynôme du second degré à l’aide de la minimisation de l’erreur ![]() des statistiques issues de ces régions homogènes.
des statistiques issues de ces régions homogènes.
Publications associées :
1. C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation of the noise level function based on a non-parametric detection of homogeneous image regions. Submitted to Siam Journal on Imaging Sciences, 2015.
2. C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation du niveau de bruit par la détection non paramétrique de zones homogènes. Submitted to Gretsi, 2015.
Références
[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.
[2] Sutour, C., Deledalle, C.-A., and Aujol, J.-F. (2014). Adaptive regularization of the NL-means: Application to image and video denoising. Preprint.
[3] M.G. Kendall, A new measure of rank correlation, Biometrika, 30 (1938), pp. 81–93.