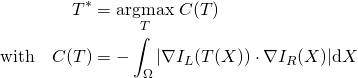Super-résolution et inpainting

Moncef Hidane a effectué un post-doctorat de 2013 à 2014 dans le cadre du Labex CPU. Il a au préalable effectué une thèse de doctorat au laboratoire GREYC à Caen, sur la problématique de décompositions de signaux sur graphes. Il est aujourd’hui enseignant chercheur à l’INSA Centre Val de Loire.

Le sujet du post-doc porte sur la reconstruction d’images 3D à partir d’une acquisition complète en basse résolution et d’une acquisition partielle en très haute résolution. Il s’agit donc d’un problème inverse de super-résolution.

Le modèle adopté pour l’acquisition basse résolution est celui d’une convolution suivie d’un opérateur de sous-échantillonage spatial ou spectral. Dans un premier temps, la réponse impulsionnelle du capteur est supposée connue. Un bruit blanc additif est intégré au modèle.

Le modèle adopté pour l’acquisition haute résolution est celui d’une occlusion dont le support est connue. Un bruit blanc additif est également intégré au modèle.

La première piste suivie est celle d’une régularisation à l’aide d’un a priori de variation totale isotrope. Deux versions sont envisagées : d’une part avec des contraintes d’inégalité, d’autre part avec des contraintes d’égalité. Dans ce cadre, une partie importante du travail concerne la minimisation des critères dans chaque cas. Du fait de la non différentiabilité de la mesure variation totale, des algorithmes issues de l’optimisation convexe non lisse sont considérés. Le but est de pouvoir disposer d’algorithmes rapides et robustes pour le calcul des solutions.

La deuxième piste suivie est un régularisation à l’aide d’un opérateur non local. L’idée est tirer partie à la fois du volume basse résolution et des images haute résolution pour construire un a priori de régularisation de type variation totale non locale.

La figure suivante illustre la problématique ainsi que les résultats obtenus avec les deux approches précédentes.

(a) image originale 256 x 256; (b) image BR (facteur 4); (c) image HR partielle; (d) interpolation bicubique de (b) (psnr=24.43); (e) reconstruction TV (psnr=29.52); (f) recontruction par régularisation non locale (psnr=30.16).

(a) image originale 256 x 256; (b) image BR (facteur 4); (c) image HR partielle; (d) interpolation bicubique de (b) (psnr=24.43); (e) reconstruction TV (psnr=29.52); (f) recontruction par régularisation non locale (psnr=30.16).

Etude des méthodes parcimonieuse pour la tomographie

Dans le cadre de la tomographie avec un nombre limité d’angles, le problème inverse résultant est mal conditionné. Les algorithmes « classiques », analytiques et algébriques, produisent de nombreux artefacts. Les méthodes d’optimisation permettent de résoudre ce problème à l’aide d’une régularisation. Dans mes travaux, je suppose les images parcimonieuses ou parcimonieuses dans une représentation donnée. Une image parcimonieuse est une image qui possède peu de composantes non nulles. Pour promouvoir cette parcimonie, je vais régulariser le problème avec une norme \ell^1 et résoudre l’un des deux problèmes équivalents ci dessous.

(1)   \begin{equation*} \underset{x\in \mathbb{R}^n}{\text{min}}\ \|x\|_1 \text{ s.t. } \|\mathbf{A}x-y\|_2\le \delta \end{equation*}

(2)   \begin{equation*} \underset{x\in \mathbb{R}^n}{\text{min}}\ \frac{1}{2}\|\mathbf{A}x-y\|_2 + \lambda \|x\|_1 \end{equation*}

Mon travail consiste à évaluer les limites théoriques de ces problèmes tout en étant le plus proche de la réalité. De récents travaux [3] ont mis en lumière des conditions suffisantes assurant la reconstruction de l’image par minimisation \ell^1 et fournissent une erreur de cette reconstruction [1]. Ces conditions nécessitent l’existence d’un vecteur particulier appelé certificat dual. Selon les applications, il peut être possible de calculer un candidat qui sous condition sera un certificat dual [2,4].

Mes travaux couvrent essentiellement la construction de tels candidats. Je propose, dans mes travaux, une approche gloutonne de calculer un candidat qui est un certificat dual pour presque toutes les images « reconstructibles » et minimisant l’erreur théorique de reconstruction.

[1] Charles Dossal and Remi Tesson. Consistency of l1 recovery from noisy deterministic measurements. Applied and Computational Harmonic Analysis, 2013.

[2] Jean-Jacques Fuchs. Recovery of exact sparse representations in the presence of bounded noise. Information Theory, IEEE Transactions on, 51(10) :3601–3608, 2005.

[3] Markus Grasmair, Otmar Scherzer, and Markus Haltmeier. Necessary and sufficient conditions for linear convergence of l1-regularization. Commun. Pure and Appl. Math., 64(2) :161–182, 2011.

[4] Samuel Vaiter, Gabriel Peyré, Charles Dossal, and Jalal Fadili. Robust sparse analysis regularization. 2011.

Transport Optimal en Traitement d’Images

Le transport optimal est désormais un outil majeur en vision par ordinateur et en traitement d’image. Il peut être utilisé pour calculer des similarités entre descipteurs, appareiller et moyenner des descripteurs (transport discret) ou encore recaler des images (transport continu). Un défaut majeur de cet outil vient du manque de régularité des plans de transports qui entraine une faible robustesse aux données aberrantes. Le coût de calcul du transport optimal est aussi une limitation pratique à son utilisation pour des problèmes de grande dimension. Dans cet axe, nous nous intéressons donc à la définition de nouveaux algorithmes permettant de calculer des solutions de problèmes de transport optimal généralisés intégrant des contraintes de régularité.

Modèles non locaux

Les systèmes imageurs utilisés dans de nombreuses applications fournissent de grands volumes d’images aux dégradations complexes et à faible rapport signal sur bruit. Des méthodes de restauration adaptées à ces spécificités doivent être développées. La puissance de calcul aujourd’hui disponible a permis l’émergence de nouveaux paradigmes, tel que celui du « non-local » (Buades et al., 2005) offrant de très bons résultats (voir, Lebrun et al. 2012; Milanfar, 2013). Cependant, l’extension de ces méthodes, issues des mathématiques appliquées, à certaines modalités d’images est non-triviale. Cet axe s’intéresse à l’extension de ces méthodes de restauration à des modalités d’images non-conventionnelles (imagerie à faible luminosité, imagerie cohérente, tomographie, …) : présence de dégradations complexes (flou, données manquantes, bruit non-gaussien, non-stationnaire et corrélé) et besoin de calculs rapides sur de grands volumes de données.

Sélection de modèle pour l’image

Un point critique des approches en restauration d’images concerne le réglage de leurs paramètres. Lorsque l’on simule des données dégradées à partir d’une image de référence, on peut comparer l’image de référence à celle restaurée par de telles approches, et ainsi sélectionner les paramètres qui offrent la meilleure qualité de restauration. Ce réglage est bien moins évident dans le cas de données réelles pour lesquelles il n’y a pas d’image de référence. Dans le cas de dégradations simples, des outils de statistique permettent d’estimer l’erreur quadratique de restauration quand bien même l’image de référence est inconnue, on parle d’« estimation de risque ». Optimiser cette estimation par rapport aux paramètres de la méthode permet alors d’obtenir une calibration proche de l’optimal. L’estimateur de risque non-biasé de Stein (SURE, Stein 1981) est l’un des exemples les plus connus, appliqué avec succès pour calibrer des méthodes de restauration d’images en présence de bruits gaussiens (par ex., Ramani et al., 2008). Nous nous intéressons dans cet axe au développement d’estimateurs dérivés du SURE pour la calibration des paramètres intervenant dans les méthodes récentes, potentiellement hautement paramétriques, pour la restauration d’images aux dégradations complexes (flou, données manquantes, bruit non-gaussien, non-stationnaire et corrélé).

Voir:
– Stein Unbiased GrAdient estimator of the Risk
– Stein Consistent Risk Estimator for hard thresholding
– Local Behavior of Sparse Analysis Regularization

Stein Unbiased GrAdient estimator of the Risk

Les algorithmes de régularisation variationnelle résolvant des problèmes inverses mal posés impliquent généralement des opérateurs qui dépendent d’un ensemble de paramètres continus. Lorsque ces opérateurs bénéficient d’une certaine régularité (locale), ces paramètres peuvent être sélectionnés en utilisant l’estimateur non-biasé de Stein (SURE). Bien que cette sélection est généralement effectuée par une recherche exhaustive, nous abordons dans ce travail le problème de l’utilisation du SURE pour l’optimisation efficace d’une collection de paramètres continus du modèle. Lorsque l’on considère des regularizations non lisses, comme la norme l1 populaire correspondant au seuillage doux, le SURE est une fonction discontinue de paramètres qui empêchent l’utilisation de techniques d’optimisation de descente de gradient. Au lieu de cela, nous nous concentrons sur une approximation du SURE sur la base de différences finies comme proposé dans (Ramani et al., 2008). Sous des hypothèses modérées sur l’estimateur, nous montrons que cette approximation est une fonction faiblement différentiables des paramètres et que son gradient faible (SUGAR), fournit asymptotiquement (par rapport à la dimension de données) une estimation non biaisée du gradient du risque. En outre, dans le cas particulier de seuillage doux, SUGAR est avéré être aussi un estimateur consistent. Le SUGAR peut alors être utilisé comme une base pour effectuer une optimisation de type quasi-Newton. Le calcul de SUGAR repose sur la forme explicite de la différenciation (faible) de la fonction non-lisse. Nous fournissons son expression pour une large classe de méthodes proximales itératives et appliquons notre stratégie à des régularisations impliquant des pénalités convexes non lisse. Des illustrations sur divers problèmes de restauration d’image et de complétion de matrices sont donnés.

Publications et codes sources associés :

Charles-Alban Deledalle, Samuel Vaiter, Gabriel Peyré and Jalal Fadili
Stein Unbiased GrAdient estimator of the Risk (SUGAR) for multiple parameter selection,
Technical report HAL, hal-00987295 (HAL)

MATLAB source codes available from GitHub.

Recalage multi-modal basé contours

Afin d’effectuer la fusion multi-modale entre les images obtenues à partir d’un intensificateur de lumière (LI) et IR (images infra-rouge), fournissant ainsi des informations multi-sources pour le pilote, il est nécessaire d’effectuer le recalage entre les deux modalités. Elles reflètent des propriétés différentes de la scène, de sorte que la méthode choisie est basée sur l’information géométrique et les bords de chaque image.

Le but est de trouver la transformation T ^ * qui transfère l’image IL dans le cadre de référence de l’image IR en minimisant l’énergie suivante:

(1)   \begin{align*} T^* &= \underset{T}{\operatorname{argmax}} \; C(T)\\ \text{with} \quad C(T) &= - \int_{\Omega} \vert \nabla I_L(T(X)) \cdot \nabla I_R(X)\vert \mathrm dX \end{align*}

Cette mesure est basée sur les contours de chaque image, et elle prend en compte les contours des deux modalitites, ce qui la rend insensible aux valeurs aberrantes.
Grâce à un schéma d’optimisation à base de descente de gradient, il est possible d’évaluer rapidement la transformation optimale entre les deux modalités.

Résultats de recalage sur des données réelles

Related papers:
C. Sutour, J.-F. Aujol, C.-A. Deledalle et B.D. De-Senneville. Edge-based multi-modal registration and application for night vision devices. Journal of Mathematical Imaging and Vision, pages 1–20, 2015.

NL-SAR: Non-Local framework for (Pol)(In)SAR denoising

Logiciel ouvert distribué sous licence CeCILL pour l’estimation adaptative et non-locale d’images (Pol)(In)SAR (réduction de speckle). Interface disponible en ligne de commande, IDL, Matlab, Python et en tant que bibliothèque dynamique C. Plug in pour PolSARpro disponible.

Téléchargement ici