Numerical night vision system:
Automatic restoration and multimodal registration of low light level images.
This work is part of Camille Sutour’s PhD entitled “Numerical night vision system: automatic restoration and multimodal registration of low light level images.”. This PhD is financed by the DGA and the Aquitaine and it is the result of a collaboration with Thales Avionics in Le Haillan. The goal of this project is to enhance the quality of night vision for helicopter pilotes. This is achieved thanks to a numerical system composed of a light intensifier (IL) coupled to a CCD camera. The obtained images are directly projected onto the helmet visor. Current studies first consist in enhancing the quality of theses IL images by performing denoising. Then the goal is to register these IL images with infra-red (IR) images to proceed to image fusion. This work lies within an operational context where videos are processed with a strong real-time constraint.

Processing of night-vision images. (a) IL raw image, (b) Denoised IL image, to register ; the edges of the IR reference image are super-imposed, (c) Registered IL image onto the reference IR image, (d) IR image.
R-NL : Regularized NL-means
Matlab implementation of the R-NL algorithm
Results of video denoising with R-NL and comparisons
The denoising algorithm that has been developed is based on an adaptive regularization of the NL-means [1]. The proposed model is the following [2]:
(1) 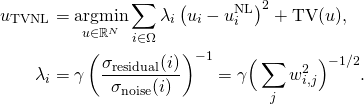
where ![]() is the solution obtained with the NL-means algorithm, TV refers to the total variation of the image and
is the solution obtained with the NL-means algorithm, TV refers to the total variation of the image and ![]() is the weight that measures the similarity between the patch of index
is the weight that measures the similarity between the patch of index ![]() and the patch of index
and the patch of index ![]() in the NL-means algorithm. The ratio
in the NL-means algorithm. The ratio ![]() reflects the noise variance reduction performed by the NL-means. This formulation allows locally adaptive regularization of the NL-means solution
reflects the noise variance reduction performed by the NL-means. This formulation allows locally adaptive regularization of the NL-means solution ![]() , thanks to a confidence index
, thanks to a confidence index ![]() that reflects the quality of the denoising performed by the NL-means.
that reflects the quality of the denoising performed by the NL-means.
This model can be adapted to the different noise statistics belonging to the exponential family (Gaussian, Poisson, multiplicative…). It can also be adapted to video denoising thanks to the use of 3D patches combined to a spatio-temporal TV regularization.
Related papers:
1. C. Sutour, C.-A. Deledalle et J.-F. Aujol. Adaptive regularization of the NL-means : Application to image and video denoising. IEEE Transactions on image processing, vol. 23(8) : 3506-3521, 2014.
2. C. Sutour, J.-F. Aujol, C.-A. Deledalle et J.-P. Domenger. Adaptive regularization of the NL-means for video denoising. International Conference on Image Processing (ICIP), pages 2704–2708. IEEE, 2014.
3. C. Sutour, J.-F. Aujol et C.-A. Deledalle. TV-NL : Une coopération entre les NL-means et les méthodes variationnelles. Gretsi, 2013.
More information and results about R-NL
Multi-modal registration
Registration results on real data
In order to perform multi-modal fusion between IL and IR (infra-red) images, hence providing multi-sources information to the pilot, it is necessary to perform registration between the two modalities. They reflect different properties of the scene, so the selected approach is based on the geometric information and the edges of each image.
The goal is to find the transformation ![]() that transfers the IL image into the frame of reference of the IR image by minimizing the following energy:
that transfers the IL image into the frame of reference of the IR image by minimizing the following energy:
(2) 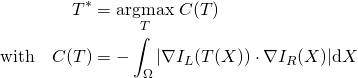
This metric is based on the edges of each image, and it only takes into account the edges that occur in both modalitites, which makes it insensitive to outliers.
Thanks to a gradient descent based optimization scheme, it is possible to quickly evaluate to optimal transformation between the two modalities.
Related papers:
C. Sutour, J.-F. Aujol, C.-A. Deledalle et B.D. De-Senneville. Edge-based multi-modal registration and application for night vision devices. Journal of Mathematical Imaging and Vision, pages 1–20, 2015.
More information and results about the multi-modal registration
Non parametric noise estimation
Matlab implementation of the noise estimation algorithm
In order to provide a fully automatic denoising algorithm, we have developed an automatic noise estimation method that relies on the non-parametric detection of homogeneous areas.
First, the homogeneous regions of the image are detected by computing Kendall’s rank correlation coefficient [3]. Computed on neighboring pixel sequences, it indicates the dependancy between neighbors, hence reflects the presence of structure inside an image block. This test is non-parametric, so the performance of the detection is independant of the noise statistical distribution.
Once the homogeneous areas are detected, the noise level function, i.e., the function of the noise variance with respect to the image intensities, is estimated as a second order polynomial minimizing the ![]() error on the statistics of these regions.
error on the statistics of these regions.
Related papers:
1. C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation of the noise level function based on a non-parametric detection of homogeneous image regions. Submitted to Siam Journal on Imaging Sciences, 2015.
2. C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation du niveau de bruit par la détection non paramétrique de zones homogènes. Submitted to Gretsi, 2015.
References
[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.
[2] Sutour, C., Deledalle, C.-A., and Aujol, J.-F. (2014). Adaptive regularization of the NL-means: Application to image and video denoising. IEEE Transactions on image processing, vol. 23(8) : 3506-3521, 2014.
[3] M.G. Kendall, A new measure of rank correlation, Biometrika, 30 (1938), pp. 81–93.