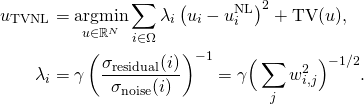Estimation de coûts au sens de Kullback-Leibler

Nous abordons la question de l’estimation des coûts au sens de Kullback-Leibler comme une alternative aux coûts quadratiques dans les problèmes de reconstruction où le bruit est distribué au sein de la famille exponentielle. Nous identifions les conditions dans lesquelles ces coûts peuvent être estimés sans biais avec avec un biais contrôlée. Des simulations sur des problèmes de sélection de paramètres dans des applications de débruitage d’images avec du bruit Gamma et Poisson illustrent l’intérêt des coûts au sens de Kullback-Leibler et des estimateurs proposés.

Article disponible ici

Convergence de FISTA

Charles Dossal a démontré avec Antonin Chambolle en 2015 la convergence d’un algorithme extrêmement populaire depuis son introduction en 2008 par Beck et Teboulle (car étant extrêmement performant en pratique), l’algorithme FISTA (Fast Iterative Shrinkage Algorithm). La convergence de cet algorithme est restée un problème ouvert dans les communautés optimisation/compressed sensing/traitement d’images/machine learning pendant 7 ans, jusqu’au travail de Charles Dossal.

Scale-Space and Variational Methods

L’équipe a organisé début juin 2015 la conférence internationale SSVM 2015 (Scale-Space and Variational Methods in Image Processing) sur le bassin d’Arcachon. Plus de 120 chercheurs venus du monde entier ont participé. Les actes de la conférence ont été publiés dans un livre par Springer.

Estimation non paramétrique du bruit

Afin de fournir un algorithme de débruitage automatique, nous avons développé une méthode automatique d’estimation du bruit dans une image, basée sur la détection non paramétrique des zones homogènes. Les régions homogènes de l’image sont détectées à l’aide du coefficient de corrélation de rang de Kendall [1]. Evalué sur des séquences de pixels voisins, il permet de mesurer la dépendance entre voisins et donc la présence de structure au sein d’un bloc de l’image.
Ce test est non paramétrique, donc la performance du détecteur est indépendante de la distribution statistique du bruit. Une fois les zones homogènes détectées, la fonction de niveau de bruit, c’est-à-dire la fonction reliant la variance du bruit à l’intensité sous-jacente de l’image, est estimée sous forme d’un polynôme du second degré à l’aide de la minimisation de l’erreur \ell^1 des statistiques issues de ces régions homogènes.

Codes Matlab pour l’estimation de bruit

Publications associées :

– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation of the noise level function based on a non-parametric detection of homogeneous image regions. Submitted to Siam Journal on Imaging Sciences, 2015.

– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation du niveau de bruit par la détection non paramétrique de zones homogènes. Submitted to Gretsi, 2015.

Références

[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.

Régularisation adaptative des NL-means

L’algorithme de débruitage mis en place repose sur une régularisation adaptative de l’algorithme des NL-means [1]. Le modèle proposé est le suivant :

(1)   \begin{align*} u_{\text{TVNL}} &= \underset{u \in \mathbb{R}^N}{\operatorname{argmin}} \sum_{i \in \Omega} \lambda_i \left(u_i-u^{\text{NL}}_i\right)^2 + \text{TV}(u),\\ \lambda_i &= \gamma \left(\frac{\sigma_{\text{residual}}(i)}{\sigma_{\text{noise}}(i)}\right)^{-1} = \gamma \Big(\sum_j w_{i,j}^2\Big)^{-1/2}. \end{align*}

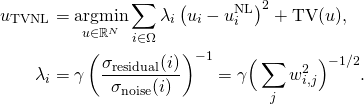
où 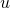u_{\NL} est la solution obtenue par l’algorithme de NL-means, TV désigne la variation totale de l’image et 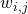w_{i,j} est le poids qui mesure la similarité entre le patch d’indice 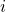i et le patch d’indice 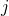j dans l’algorithme des NL-means. Le rapport 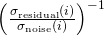\left(\frac{\sigma_{\text{residual}}(i)}{\sigma_{\text{noise}}(i)}\right)^{-1} traduit la réduction de la variance du bruit assurée par les NL-means. Cette formulation permet de régulariser localement et de façon adaptative la solution 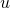u_{\NL} obtenue par les NL-means, en se basant sur un indice de confiance 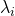\lambda_i qui traduit la qualité du débruitage effectué par les NL-means.

Ce modèle s’adapte aux différentes statistiques de bruit de la famille exponentielle (Gaussien, Poisson, multiplicatif…). Il est également adapté au débruitage vidéo grâce à l’utilisation de patchs 3D combinée à une régularisation TV spatio-temporelle.

Codes Matlab pour RNL

Résultats et comparaisons de débruitage de vidéos avec R-NL

Publications asosciées :
– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Adaptive regularization of the NL-means : Application to image and video denoising. IEEE Transactions on image processing, vol. 23(8) : 3506-3521, 2014.

– C. Sutour, J.-F. Aujol, C.-A. Deledalle et J.-P. Domenger. Adaptive regularization of the NL-means for video denoising. International Conference on Image Processing (ICIP), pages 2704–2708. IEEE, 2014.

– C. Sutour, J.-F. Aujol et C.-A. Deledalle. TV-NL : Une coopération entre les NL-means et les méthodes variationnelles. Gretsi, 2013.

Références

[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.

Relaxations de fonctionnelles non-convexes

Nous étudions différentes relaxations pour minimiser des fonctionnelles non convexes qui apparaissent en traitement d’images. Des problèmes comme la segmentation d’image peuvent en effet s’écrire comme un problème de minimisation d’une certaine fonctionnelle, le minimiseur représentant la segmentation recherchée.

Différentes méthodes ont été proposées pour trouver des minima locaux ou globaux de la fonctionnelle non convexe du modèle de Mumford-Shah constant par morceaux à deux phases. Certaines approches utilisent une relaxation convexe qui permet d’obtenir des minima globaux de la fonctionnelle non convexe. On rappelle et compare certaines de ces méthodes et on propose un nouveau modèle par bande étroite, qui permet d’obtenir des minima locaux tout en utilisant des algorithmes robustes qui proviennent de l’optimisation convexe. Ensuite, on construit une relaxation convexe d’un modèle de segmentation à deux phases qui repose sur la comparaison entre deux histogrammes donnés et les histogrammes estimés globalement sur les deux régions de la segmentation.

Des relaxations pour des problèmes multi-étiquettes à plusieurs dimensions comme le flot optique sont également étudiées. On propose une relaxation convexe avec un algorithme itératif qui ne comprend que des projections qui se calculent exactement, ainsi qu’un nouvel algorithme pour une relaxation convexe sur chaque variable mais non convexe globalement. On étudie la manière d’estimer une solution du problème non convexe original à partir d’une solution d’un problème relaxé en comparant des méthodes existantes avec des nouvelles.

Colorisation d’images

La colorisation est un enjeu important pour la restauration des documents anciens par exemple, mais également pour l’industrie du divertissement. Les méthodes se divisent en deux catégories, les méthodes manuelles et les méthodes dites basée-exemple pour lesquelles l’utilisateur fournit une image en couleur qui sert de source d’information. La comparaison des textures permet d’extraire la couleur. Il faut ensuite régulariser, ce que l’on effectue dans notre cas par la minimisation d’une fonctionnelle non convexe. Proposer un modèle raisonnable pour la colorisation ainsi qu’un algorithme efficace pour minimiser la fonctionnelle proposée a constitué l’essentiel du début de la thèse.

Néanmoins, les méthodes basée-exemple présentent une difficulté qui est la recherche d’une image source pertinente. Il est difficile de trouver l’image source pertinente pour une colorisation donnée, et la méthode échoue fréquemment, il suffit par exemple qu’une couleur ne soit pas présente dans l’image source, ou encore d’avoir deux parties lisses ou des textures similaires devant exprimer une couleur différente. Afin d’éviter ces écueils, nous avons proposé une méthode de colorisation dite collaborative, qui se présente comme une méthode interactive dans laquelle l’utilisateur tiens un rôle de superviseur du résultat. Il a la possibilité d’intégrer des points de couleurs dans le résultat là où le résultat ne lui semble pas satisfaisant. Cette nouvelle information est intégrée dans le processus en exploitant la non convexité du modèle.

Illustration de Colorisation